

A knapsack problem includes a given set of items having. We introduce a new algorithm that achieves aĬompetitive ratio within an additive factor of one of the best achievableĬompetitive ratios for the general problem and matches or improves upon theīest-known competitive ratio for special cases in the knapsack and one-way Knapsack problems are combinatorial optimization problems used to illustrate both problem and solution. Separately, and additionally finds application to the real-time control ofĮlectric vehicle (EV) charging. Problem and of the one-way trading problem that have previously been treated This problem generalizes variations of the knapsack Problem with multiple knapsacks, heterogeneous constraints on which items canīe assigned to which knapsack, and rate-limiting constraints on the assignment
#Knapsack algorithm pdf
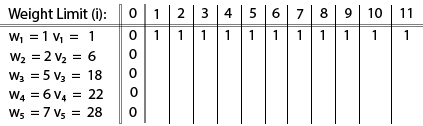
Tsang Download PDF Abstract: We introduce and study a general version of the fractional online knapsack Finally return the maximum value we get by picking or leaving the current item.Authors: Bo Sun, Ali Zeynali, Tongxin Li, Mohammad Hajiesmaili, Adam Wierman, Danny H.K.Leave the current item from knapsack and recur for remaining items.Pick the current item and recur for the remaining items with the reduced capacity of knapsack until the capacity becomes negative.This problem can be solved using recursion, considering that for each item there will be two outcomes. So the maximum value we will get is 12(4) + 1(1) + 4(10) = 17 Example (Bounded) Input:Īs our capacity is 15, we can add weights (4 + 1 + 10 = 15) It is a combinatorial optimization problem and highly used in resource allocation where a task has to be chosen as a whole from a project or task under fixed budget or constraints. Un-Bounded knapsack: Items can be repeated.Bounded knapsack: Items cannot be repeated.It has two variations depending upon how we use the items. There is another variation of this known as fractional knapsack where you can break the items. The knapsack problem or rucksack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the. Let us discuss the Knapsack problem in detail. Although the same problem could be solved by employing other algorithmic approaches, Greedy approach solves Fractional Knapsack problem reasonably in a good time. In this kind of problem, there are set of items are given with a weight and a value. The Greedy algorithm could be understood very well with a well-known problem referred to as Knapsack problem. The knapsack problem or rucksack problem is a problem in combinative or integrative optimization. Submitted by Abhishek Kataria, on AugKnapsack problem. There is a single constraint to this problem, you cannot break an item, either pick the complete item or don’t pick it (0-1 property). Algorithm for fractional knapsack with its example is also prescribed in this article. This is a typical unbounded knapsack problem where you can pack as many as items per item-type as long as there is enough capacity. int weights array with the weights of all items. Unbounded Knapsack Problem solved by Dynamic Programming Algorithm.

We are given different items, each having a certain weight and a value, we have to pick items in the knapsack such that the values of those items are as large as possible, but their weight should be within the limit of knapsack, it should not exceed it. The parameters of function knapsack are: int index index of the item you need to decide to take or not (we start with the last element of the array and we work toward the first) int size size still available at the backpack. The knapsack problem is inspired by a task where we are given a limited size knapsack and it must be filled with most valuable items.


 0 kommentar(er)
0 kommentar(er)
